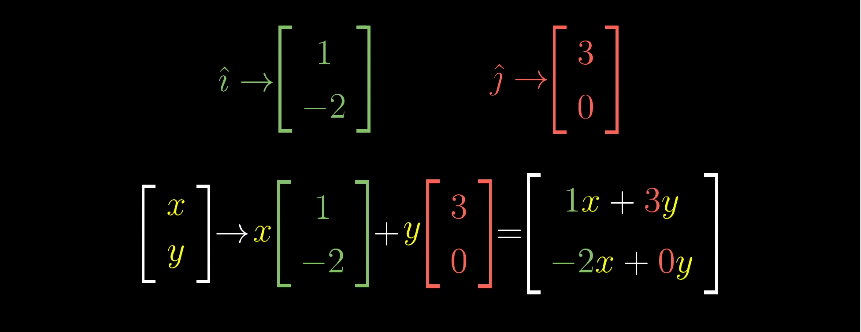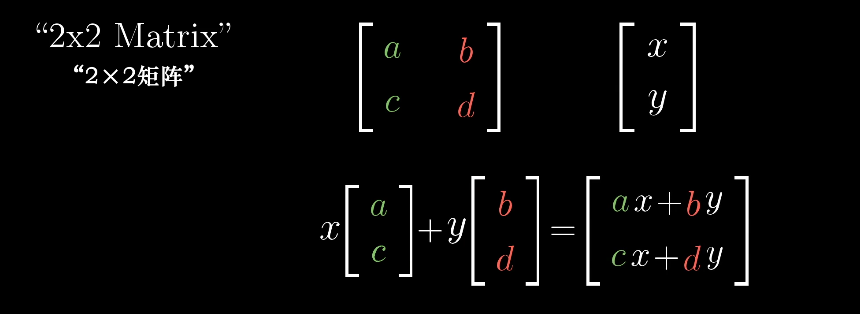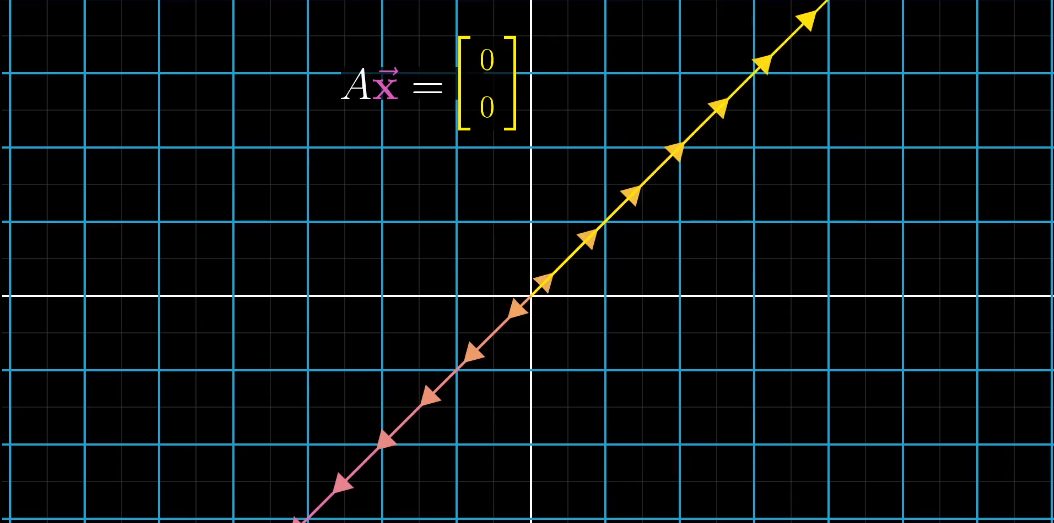说明
上线代课的时候,觉得老师讲的特别枯燥无味。直到最近在B站看了“线性代数的本质”的视频,才发现线性代数其实蛮好玩的。
视频链接
向量究竟是什么
三种观点
物理:向量是空间中的箭头
计算机:向量是有序的数字列表
数学:向量可以是任何东西,只要保证两个向量相加以及数字和向量相乘有意义即可。
线性组合、张成的空间
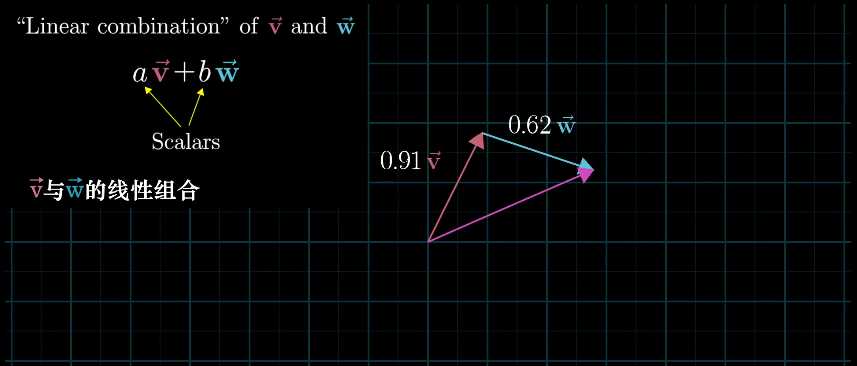
线性组合
“将向量进行缩放再相加” 这种操作称为线性组合
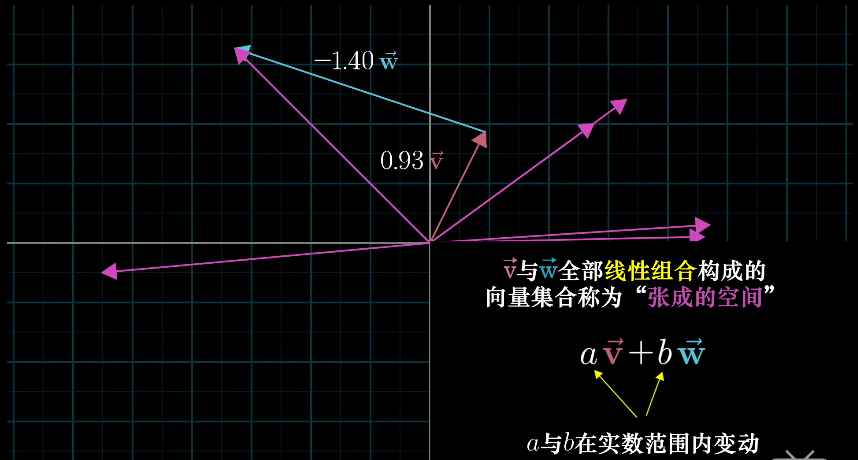
张成的空间
v, w 的 全部线性组合 所构成的向量集合称为向量 v, w 所张成的空间。
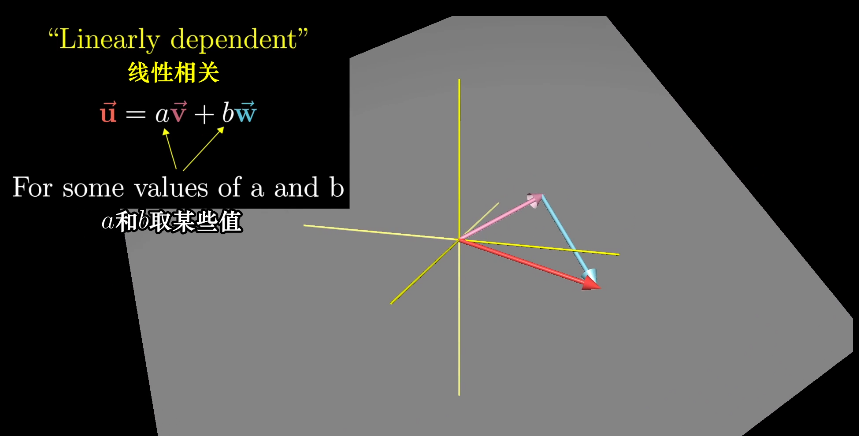
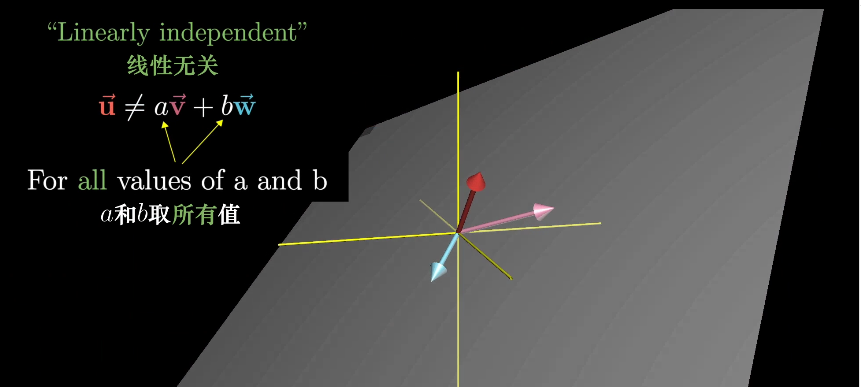
线性相关和线性无关
基的严格定义
矩阵与线性变换
输入一个向量,会输出另一个向量
变换前:白色方格
变换后:蓝色菱形
线性变换的充要条件
1、变换前后,所有的直线仍是直线
2、变换前后,原点保持不变
用矩阵表示
一般形式
二维旋转矩阵
$\begin{bmatrix} cos\theta&-sin\theta \sin\theta\ & cos\theta \ \end{bmatrix} $
将坐标轴逆时针旋转$\theta$角度,向量$i$(1,0)就 变成了($cos\theta,sin\theta$),向量$j$(0,1)就 变成了($-sin\theta,cos\theta$)。
矩阵乘法与线性变换复合
矩阵相乘的几何意义
矩阵相乘的几何意义,就是线性变换的复合。

要从右往左读,因为Shear和Rotation乘的几何意义是先旋转变换再剪切变换。显然先Shear和先Rotation的效果是不一样的,这也是为什么矩阵乘法中AB$\neq$BA。
矩阵结合率的证明
为什么(AB)C=A(BC)?哈哈哈,答案很简单,因为它们从右往左读是一样的!都是由C$\rightarrow$B$\rightarrow$A的线性变换!
(这里吐槽一下上课学的线代,证明的时候就给个矩阵让你自己推一遍,根本不知道为什么)
行列式
行列式的几何意义
线性变换对面积产生改变的比例(也可以为负值,即空间取向发生了反转),称为这个变换的行列式。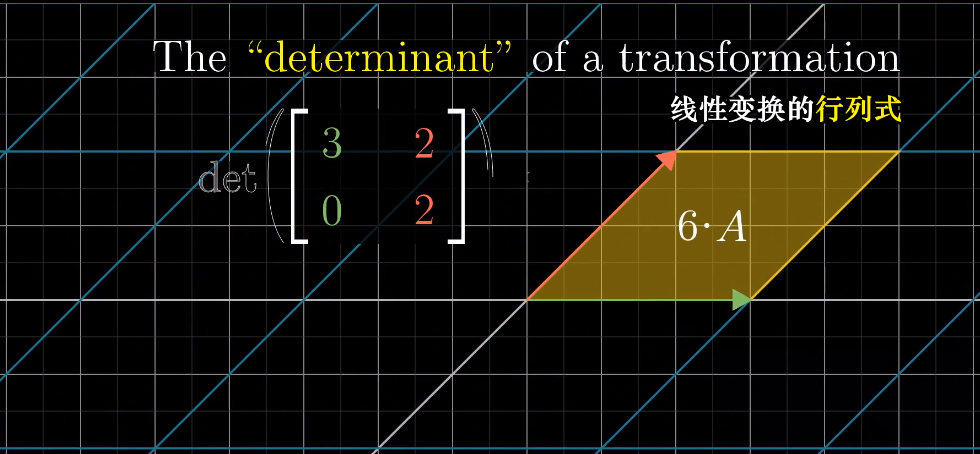
理解他的意义比计算重要得多。
行列式等于零,意味着这个矩阵所代表的变换将空间压缩到了更小的维度上。(两个向量共线了)
det(AB)=det(A)*det(B) 为什么?
因为det(AB)表示经过AB两次缩放后的面积,det(A)*det(B)表示先A后B放缩后的面积,本质上是一样的。
逆矩阵、列空间与零空间
逆矩阵
如果一个矩阵$A$把向量$x$变成了向量$v$,那么逆矩阵$A^{-1}$表示把向量$v$变成了向量$x$的线性变换。
$AA^{-1}=E$,因为$AA^{-1}$因为把一个向量变过去又变过来,相当于什么都没做。这被称为恒等变换。
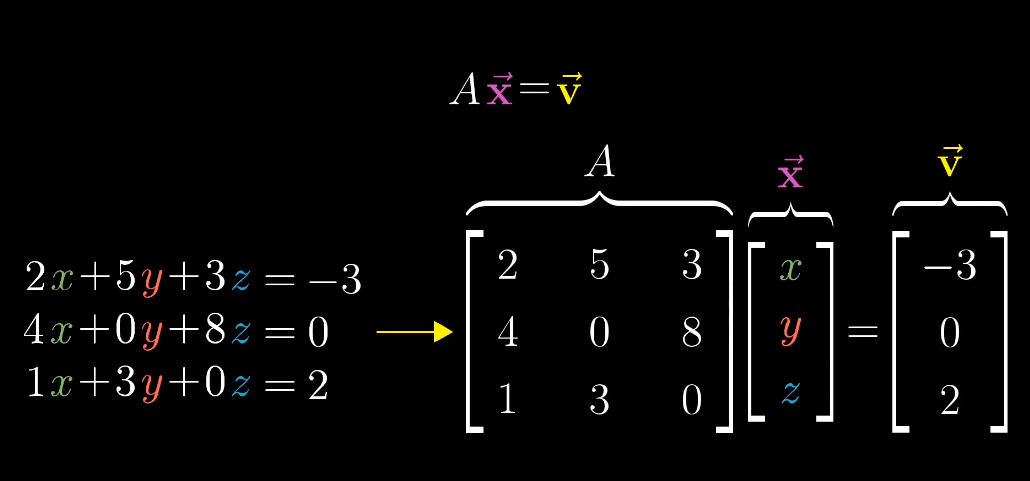
线性方程组的求解
两边同时乘以$A^{-1}$:
$A^{-1}Ax = A^{-1}v$
即
$x = A^{-1}v$
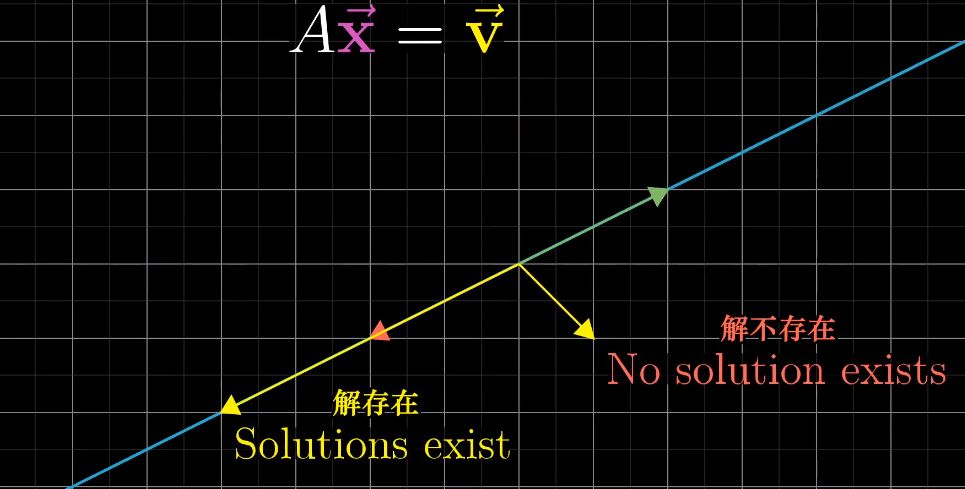
只要$A$不将空间压缩到更低的维度上,那就存在$A^{-1}$。(如果$A$的行列式为0,那就说明A变换将空间的维度变低了,就变不回去了,$A^{-1}$也就不存在了)
(嗯,降维打击是不可逆的!)
当然,$A$的行列式等于0时,$x$也是有可能有解的(足够幸运的话)即$x$和$v$共线时,即使降维也可以变过去!
矩阵的秩
其实秩代表的就是变换空间的维度啦。。这样就好理解了。。。
$R(A) = 0 $ 点
$R(A) = 1$ 直线
$R(A) = 2 $ 平面
$R(A) = 3 $ 空间
列空间
不管是一条直线、一个平面还是三维空间等,所有可能的变换结果的集合,被称为矩阵的列空间。
列空间就是矩阵的列张成的空间。
为什么叫列空间??
因为矩阵的列可以告诉我们基向量变换后的位置,这些变换后的基向量张成的空间就是所有可能的变换结果。
所以,秩的更精确的定义是列空间的维数。
零空间
变换后落在原点的向量的集合,成为“零空间”或“核”。
对于线性方程组,当向量$v$为0时,即$Ax = 0$时,零空间给出的就是这个线性方程组所有可能的解。
点积与对偶性
一个向量的对偶是它定义的线性变换。
一个多维空间到一维空间的线性变换的对偶是多维空间中的某个特定向量。
两个向量点积,就是将其中一个转化为线性变换。这个证明有点强,建议看视频!